Basics of parameter estimation

In this example, we’ll go into some of the basics of parameter estimation and how they are implemented in bilby.

Firstly, consider a situation where you have discrete data \(\{y_0, y_1,\ldots, y_n\}\) taken at a set of times \(\{t_0, t_1, \ldots, t_n\}\). Further, we know that this data is generated by a process which can be modelled by a linear function of the form \(y(t) = m t + c\). We will refer to this model as \(H\). Given a set of data, how can we figure out the coefficients \(m\) and \(c\)?

This is a well studied problem known as linear regression and there already exists many ways to estimate the coefficients (you may already be familiar with a least squares estimator for example).

Here, we will describe a Bayesian approach using nested sampling which might feel like overkill for this problem. However, it is a useful way to introduce some of the basic features of bilby before seeing them in more complicated settings.

The maths

Given the data, the posterior distribution for the model parameters is given by

\[P(m, c| \{y_i, t_i\}, H) \propto P(\{y_i, t_i\}| m, c, H) \times P(m, c| H)\,.\]

where the first term on the right-hand-side is the likelihood while the second is the prior. In the model \(H\), the likelihood of the data point \(y_i, t_i\), given a value for the coefficients we will define to be Gaussian distributed as such:

\[P(y_i, t_i| m, c, H) = \frac{1}{\sqrt{2\pi\sigma^2}} \mathrm{exp}\left(\frac{-(y_i - (t_i m + c))^2}{2\sigma^2}\right) \,.\]

Next, we assume that all data points are independent. As such,

\[P(\{y_i, t_i\}| m, c, H) = \prod_{i=1}^n P(y_i, t_i| m, c, H) \,.\]

When solving problems on a computer, it is often convenient to work with the log-likelihood. Indeed, a bilby likelihood must have a log_likelihood() method. For the normal distribution, the log-likelihood for n data points is

\[\log(P(\{y_i, t_i\}| m, c, H)) = -\frac{1}{2}\left[ \sum_{i=1}^n \left(\frac{(y_i - (t_i x + c))}{\sigma}\right)^2 + n\log\left(2\pi\sigma^2\right)\right] \,.\]

Finally, we need to specify a prior. In this case we will use uncorrelated uniform priors

\[P(m, c| H) = P(m| H) \times P(c| H) = \textrm{Unif}(0, 5) \times \textrm{Unif}(-2, 2)\,.\]

The choice of prior in general should be guided by physical knowledge about the system and not the data in question.

The key point to take away here is that the likelihood and prior are the inputs to figuring out the posterior. There are many ways to go about this, we will now show how to do so in bilby. In this case, we explicitly show how to write the GaussianLikelihood so that one can see how the maths above gets implemented. For the prior, this is done implicitly by the naming of the priors.

The code

In the following example, also available under examples/core_examples/linear_regression.py we will step through the process of generating some simulated data, writing a likelihood and prior, and running nested sampling using bilby.

#!/usr/bin/env python
"""
An example of how to use bilby to perform parameter estimation for
non-gravitational wave data. In this case, fitting a linear function to
data with background Gaussian noise

"""
import bilby
import matplotlib.pyplot as plt
import numpy as np

# A few simple setup steps
label = "linear_regression"
outdir = "outdir"
bilby.utils.check_directory_exists_and_if_not_mkdir(outdir)


# First, we define our "signal model", in this case a simple linear function
def model(time, m, c):
    return time * m + c


# Now we define the injection parameters which we make simulated data with
injection_parameters = dict(m=0.5, c=0.2)

# For this example, we'll use standard Gaussian noise

# These lines of code generate the fake data. Note the ** just unpacks the
# contents of the injection_parameters when calling the model function.
sampling_frequency = 10
time_duration = 10
time = np.arange(0, time_duration, 1 / sampling_frequency)
N = len(time)
sigma = np.random.normal(1, 0.01, N)
data = model(time, **injection_parameters) + np.random.normal(0, sigma, N)

# We quickly plot the data to check it looks sensible
fig, ax = plt.subplots()
ax.plot(time, data, "o", label="data")
ax.plot(time, model(time, **injection_parameters), "--r", label="signal")
ax.set_xlabel("time")
ax.set_ylabel("y")
ax.legend()
fig.savefig("{}/{}_data.png".format(outdir, label))

# Now lets instantiate a version of our GaussianLikelihood, giving it
# the time, data and signal model
likelihood = bilby.likelihood.GaussianLikelihood(time, data, model, sigma)

# From hereon, the syntax is exactly equivalent to other bilby examples
# We make a prior
priors = dict()
priors["m"] = bilby.core.prior.Uniform(0, 5, "m")
priors["c"] = bilby.core.prior.Uniform(-2, 2, "c")

# And run sampler
result = bilby.run_sampler(
    likelihood=likelihood,
    priors=priors,
    sampler="dynesty",
    nlive=250,
    injection_parameters=injection_parameters,
    outdir=outdir,
    label=label,
)

# Finally plot a corner plot: all outputs are stored in outdir
result.plot_corner()

Running the script above will make a few images. Firstly, the plot of the data:

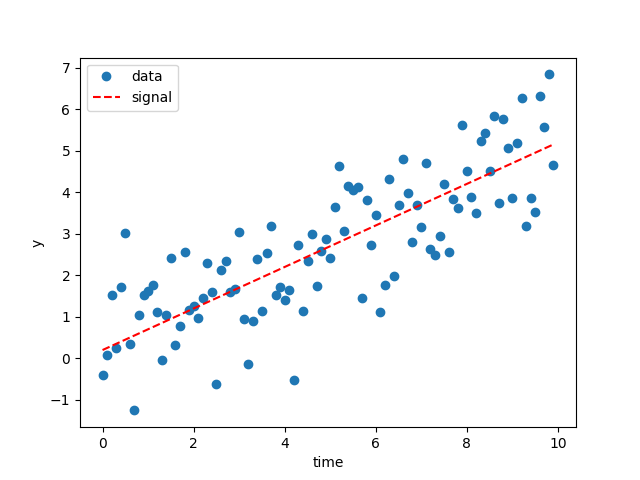
The dashed red line here shows the simulated signal.

Secondly, because we used the plot=True argument in run_sampler we generate a corner plot

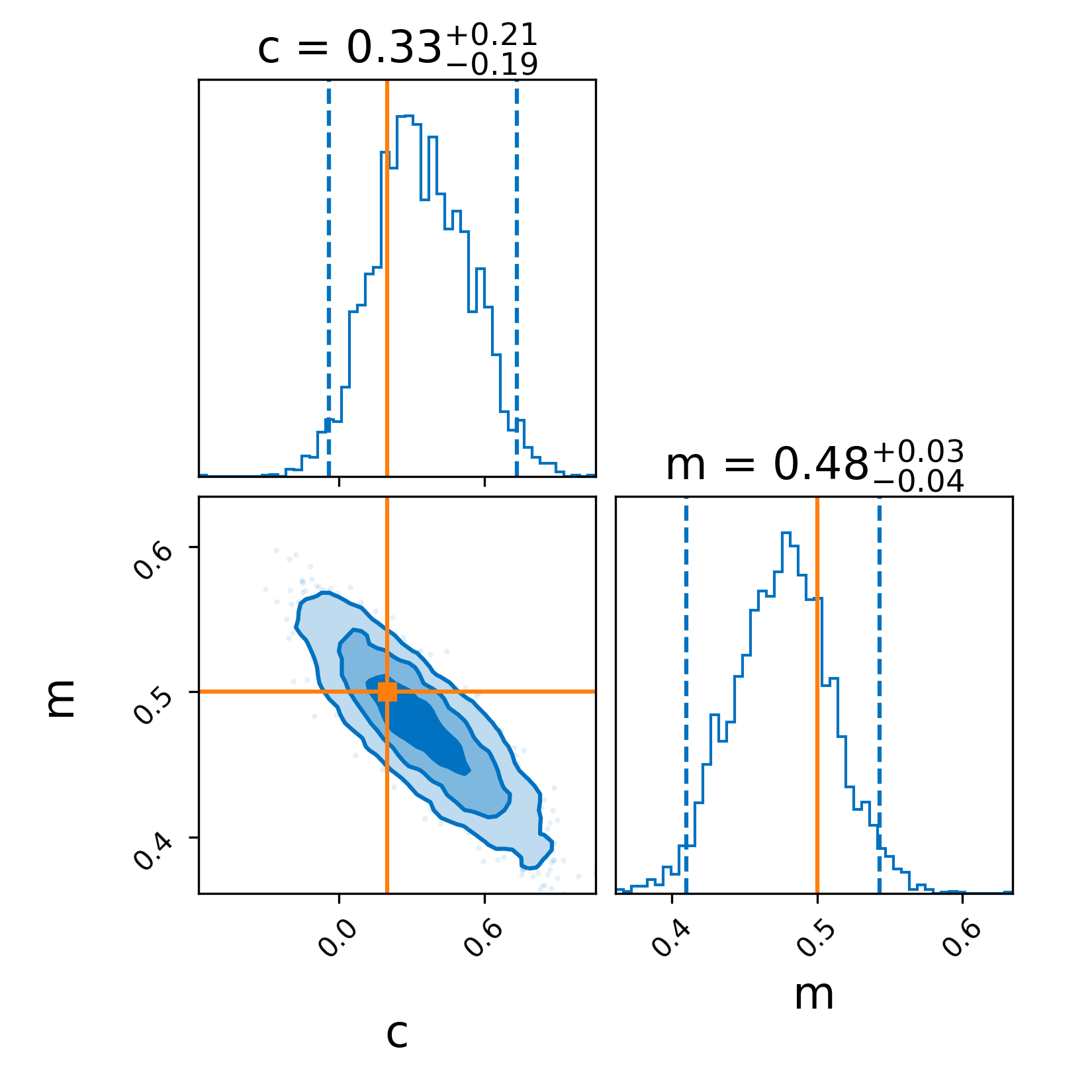
The solid lines indicate the simulated values which are recovered quite easily. Note, you can also make a corner plot with result.plot_corner().

Final thoughts

While this example is somewhat trivial, hopefully you can see how this script can be easily modified to perform parameter estimation for almost any time-domain data where you can model the background noise as Gaussian and write the signal model as a python function (i.e., replacing model).